Algorytm i człowiek

W poprzednim artykule z tej serii dowiedzieliśmy się, że niezależnie od dziedziny, algorytmy podejmują lepsze decyzje niż ludzie. Dziś przyjrzymy się badaniom, które ciągną temat jeszcze dalej.

Jedną z poważniejszych wątpliwości co do wyższości algorytmu nad osądem człowieka jest potencjalna trudność w zamodelowaniu procesów myślowych człowieka. Dzięki nieszablonowemu myśleniu, ludzie potrafią znajdować takie zależności pomiędzy danymi, które pozostają niezauważone dla nawet najlepszych algorytmów.

W uproszczeniu, na obecny moment matematycy potrafią przenieść do komputera 3 rodzaje zależności. Zaczynając od najłatwiejszej:

• zależność liniowa - spotykamy się z nią na co dzień i pomaga nam np. wybrać odpowiedni strój do wyjścia na dwór. Jeśli jest 25°C to zakładamy koszulkę. Jeśli jest 15°C to zakładamy bluzę. Jeśli jest 5°C to zakładamy kurtkę. Ogólnie im mniejsza temperatura tym grubszy jest nasz ubiór.
   
• zależność krzywoliniowa (np. parabola) - opisuje np. nasze samopoczucie na dworze. Jeśli jest 20°C to czujemy się idealnie (najwyższy punkt paraboli). Jeśli jest -10°C to nie czujemy się dobrze, bo jest nam zimno. Jeśli jest 40°C to też nie czujemy się dobrze, bo jest nam za gorąco.
   
• zależność konfigurowana - najbardziej zaawansowana zależność, która polega na tym, że nasza decyzja zależy od wzajemnej relacji dwóch czynników. Np. wybierając strój do wyjścia na dwór: jeśli jest 15°C i sucho to weźmiemy bluzę, ale jeśli jest 15°C i pada to już kurtkę. Jeśli jest 30°C i sucho to weźmiemy koszulkę, a jeśli jest 30°C i pada to i tak wystarczy nam koszulka.
  
  W tym wypadku nasza decyzja zależy nie od każdego czynnika z osoba (temperatura,deszcz), ale od ich wzajemnej kombinacji.

Oczywiście to tylko pewne matematyczne modele otaczającej nas rzeczywistości. Nasz mózg potrafi analizować dane w znacznie bardziej skomplikowane sposoby, ale na razie jako ludzie nie potrafimy przełożyć ich na język matematyki. To stąd mogłaby wynikać ewentualna przewaga człowieka nad komputerem. Oto poglądowy diagram pokazujący to z jakimi decyzjami pozwala sobie radzić ludzki mózg i algorytm.

Im niżej tym prostszy, bardziej uproszczony model rzeczywistości.

Jak duża część procesu myślowego przebiega w ramach pierwszych 3 prostokątów, które potrafimy przełożyć na algorytm?

Sprawdził to Lewis R. Goldberg w swoich badaniach prowadzonych na uniwersytecie w Oregonie. Wybrał on kilka problemów, w których eksperci musieli łączyć dane w jak najbardziej niestandardowy sposób, tak aby algorytmom było jak najtrudniej zamodelować proces dochodzenia do decyzji. Jednym z takich problemów było rozróżnianie łagodnych wrzodów żołądka od tych złośliwych na podstawie zdjęć rentgenowskich.

Żeby uświadomić sobie trudność tego zadania, musimy pamiętać, że algorytmy najlepiej pracują na danych liczbowych (np. takich jak dane finansowe spółek giełdowych). Jeśli pojawiają się dane "słowne" (np. samopoczucie pacjenta w dniu przyjęcia = "dobre"), to zanim algorytm będzie mógł je "zrozumieć", trzeba je zamienić na dane liczbowe. Można to zrobić np. tworząc skalę: (1 - bardzo słabe, 2 - słabe, 3 - średnie, 4 - dobre, 5 bardzo dobre). Należy jednak pamiętać, że taka zamiana skali słownej na liczby może być miejscem powstawania przekłamań, które później mogą wpływać na decyzje.

O ile skale słowne są dla algorytmów niewygodne (ale znośne), to zdjęcie rentgenowskie jest jeszcze wyższym poziomem trudności. Pamiętajmy, że algorytm nie ma w tym eksperymencie wglądu do zdjęcia (nie ma tu żadnego komputerowego rozpoznawania obrazu). Musi on polegać jedynie na opisie zdjęcia przez ludzi, którzy tworzą zdania w stylu: "Cecha X nie występuje".

Eksperci zajmujący się wrzodami żołądka wyszczególniają 7 cech, których należy szukać na zdjęciu rentgenowskim, z czego jedna z nich może występować tylko przy odpowiedniej konfiguracji pozostałych.

Nie ma zatem wątpliwości, że tego typu zadanie nie jest trywialne.

Goldberg stworzył różne wersje algorytmu, od najprostszego korzystającego tylko z zależności liniowych, po skomplikowane, które zawierały wielokrotne konfiguracje zmiennych. Chciał zobaczyć, który z nich i w jakim stopniu będzie w stanie zamodelować problem jak najbliżej tego jak robią to ludzie. Następnie zarówno eksperci jak i algorytmy ruszyli do pracy przy rozróżnianiu wrzodów na podstawie 192 zdjęć pacjentów.

Wyniki okazały się zaskakujące. Oto słowa autora eksperymentu:
"On the average, roughly 90% of a judge's reliable variation of response could be predicted by a simple formula combining only individual symptoms in an additive fashion and completely ignoring interractions."

Co w tłumaczeniu oznacza, że sam tylko najprostszy liniowy algorytm wyjaśnił w 90% dlaczego eksperci w danym przypadku podjęli taką a nie inną decyzję. Dodatkowo okazało się, że pozostałe 10% decyzji w pełni udało się wyjaśnić poprzez pozostałe 2 modele (krzywoliniowy i konfigurowany).

Te same badania były powtarzane dla innych problemów (np. dla odróżniania nerwicy od psychozy, o której mówiliśmy w poprzedniej części tego artykułu). Wyniki zawsze były bardzo zbliżone i wskazywały na to, że model liniowy tłumaczy od 90% do 100% procesu decyzyjnego człowieka.

Co to oznacza:

Poza-schematyczne myślenie i nie dające się opisać matematycznie procesy nie mają żadnego wpływu na skuteczność podejmowanej decyzji. Co więcej, nawet prosty liniowy model jest wystarczająco zbliżony do ludzkiego toku myślenia, aby podejmować lepsze decyzje niż człowiek. Oznacza, to że nawet prosty, pospolity algorytm będzie osiągał lepsze wyniki niż eksperci z danej dziedziny.

Ale Goldberg na tym nie poprzestał. Stwierdził, że skoro decyzje podejmowane przez ludzi dają się łatwo wyjaśnić liniowym modelem, to może odpowiednie ich uświadomienie i dodatkowy trening w łączeniu ze sobą odpowiednich przesłanek pozwoli im osiągać lepsze rezultaty. Ten test został przeprowadzony jako rozszerzenie eksperymentu nerwica/psychoza z poprzedniej części tego wpisu. Dla przypomnienia po nauce rozpoznawania nerwicy/psychozy z profili MMPI pacjentów każda z grup osiągnęła następujące rezultaty:

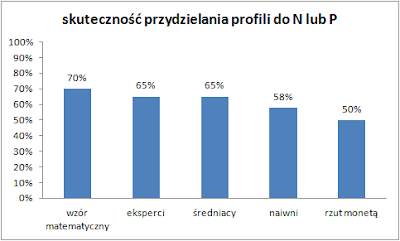
Do dalszej części eksperymentu tych samych ludzi podzielono na nowe 4 kategorie:

• standardowi - ta grupa kontynuowała rozpoznawanie profili MMPI, tak jak do tej pory. Była to grupa kontrolna
   
• wzmożony trening - ta grupa przed przystąpieniem do dalszej części eksperymentu dostała nową pulę treningowych profili MMPI do przejrzenia. Składały się one głównie z takiego rodzaju profili MMPI, których rozpoznawanie jak dotąd szło ludziom najgorzej. (Każdy profil treningowy miał z tyłu gotową odpowiedź czy jest to nerwica czy psychoza).
   
• udostępniony algorytm - ta grupa otrzymała dokładnie ten sam wzór matematyczny, którym posługiwał się algorytm (polegał on na zsumowaniu 5 konkretnych wartości z profilu MMPI) i zachęcono ich do korzystania z niego mówiąc, że może on poprawić ich osiągnięcia.
   
• konkretna wartość - ta grupa nie otrzymała wzoru, ale już gotową liczbę obliczoną przez wzór stosowany przez algorytm. Powiedziano im jaka jest wartość graniczna powyżej, której profile najprawdopodobniej są psychozą. Powiedziano im także, że im wartość jest dalej od granicy tym większa pewność diagnozy oraz, że korzystając z tego wzoru osiągną skuteczność ok. 70% (i że jest to więcej niż osiągali wcześniej). Byli także zachęcani do próby poprawy wyników wzoru (np. mogli cały czas sugerować się wzorem, ale wyłapywać przypadki dziwne, które należało osądzić na innych zasadach).

Dzięki takiemu sformułowaniu eksperymentu Golberg był w stanie sprawdzić, czy połączenie sił człowieka z algorytmem pozwoli osiągnąć jeszcze lepsze rezultaty niż w pojedynkę. Zapytałem was o wasze podejście do tego tematu w ankiecie. Oto wasze odpowiedzi:

W ankiecie wyraźnie przeważają zwolennicy łączenia człowieka z algorytmem. Aż 81% osób opowiedziało się za takim podejściem.

Oto wyniki Goldberga:

• grupy osób z konkretną wartością algorytmu zbliżyły się do skuteczności 70%, ale osiągnęły gorsze rezultaty niż gdyby po prostu korzystały z otrzymanej formuły i nie próbowały jej poprawiać subiektywnym osądem.
   
• grupy z udostępnionym algorytmem początkowo osiągały wyniki bardzo zbliżone do 70%, ale im dłużej trwał eksperyment tym bardziej ich skuteczność wracała do standardowej.
   
• grupy, które otrzymały wzmożony trening na profilach MMPI, które wcześniej sprawiały trudność nie wykazały żadnej poprawy.

Wnioski są dość okrutne dla ludzi:

• Próby ręcznej poprawy wyników algorytmu są skazane na porażkę. Algorytm radzi sobie najlepiej, gdy jego decyzje nie mogą zostać podważone przez ludzi.
   
• Wyniki grupy, która dostała do ręki wzór pozwalający poprawić wyniki oznaczają, że ludzie mają problemy z oceną, które informacje są ważne, a które nie. (po początkowej fascynacji nowymi danymi stopniowo zaprzestawali korzystania ze wzoru).
   
• Ludzie nie są w stanie pokonać pewnego poziomu skuteczności prognoz nawet po dodatkowym treningu.

Jestem ciekaw co o tym sądzicie?

Bibliografia:
Lewis R. Goldberg 1968 "Simple models or simple processes".

Jeśli wpis Ci się podoba zapisz się na newsleter, aby nie przegapić nowych artykułów:		Zapisz się