Co jakiś czas dostaję maile, w których pytacie się mnie: "Skąd wiem, że moje podejście do inwestowania jest dobre?". Być może przez cały ten czas miałem po prostu szczęście, tak jak kandydat na analityka, który miał 100% trafnych przepowiedni?
Dziś opowiem wam nieco więcej o teorii stojącej za portfelem fundamentalnym.
Branża ubezpieczeniowa jest jedną z najbardziej stabilnych i przewidywalnych. Ładnie pokazują to chociażby wykresy zysków i rentowności naszego głównego krajowego ubezpieczyciela PZU:
Biznes ubezpieczeniowy polega na tym, że klienci kupują od takiego PZU ubezpieczenie np. od kradzieży samochodu, płacąc co roku małą część jego wartości. To są przychody ubezpieczyciela. Co jakiś czas zdarzy się, że któryś samochód zostanie ukradziony i wtedy PZU musi wypłacić jego równowartość. To są koszty ubezpieczyciela. Przychody minus koszty dają zysk, a więc to co widać na wykresie powyżej jako zielone słupki.
Jak widać PZU nie ma problemu z utrzymywaniem przychodów większych niż kosztów. Jak to możliwe? Przecież wpłaty osób ubezpieczających samochody, to tylko drobna część wartości samochodu (np. 200 zł rocznie), a gdy taka kradzież się zdarzy to wypłata sięga pełnej wartości samochodu (czyli np. 100 tys. zł). Przecież PZU nie potrafi przewidywać który samochód ukradną, a którego nie.
Zrozumienie tego w jaki sposób ubezpieczyciel jest w stanie regularnie zarabiać jest kluczem do równie regularnego zarabiania na giełdzie.
Załóżmy, że Adam przychodzi do PZU i mówi im: Mam 3 letnią Skodę Octavię, którą chciałbym ubezpieczyć od kradzieży. Maksymalnie jestem gotów zapłacić za takie ubezpieczenie 100 zł rocznie, czy się zgadzacie?
Co w takiej sytuacji powinniśmy zrobić? Gdyby Adam zaproponował 1 zł rocznie to wiedzielibyśmy, że to zbyt mało, aby ponosić ryzyko tego, że samochód zostanie ukradziony i nie sprzedalibyśmy ubezpieczenia. Gdyby Adam zaproponował 10 tys. zł rocznie to wiedzielibyśmy, że to dużo w stosunku do ryzyka, że samochód zostanie ukradziony i wtedy sprzedalibyśmy takie ubezpieczenie. Ale gdzie jest granica pomiędzy zbyt mało, a zbyt dużo? Spójrzmy jak tę granicę znajdują profesjonaliści.
Profesjonaliści najpierw zbierają informację o wszystkich kradzieżach w Polsce w ciągu kilku / kilkunastu lat. Szczególnie interesuje ich to jaki samochód został ukradziony (model, rocznik), w jakich okolicznościach doszło do zdarzenia (pod domem, na mieście itp.), w jakim mieście / dzielnicy doszło do kradzieży itp.
Powstaje z tego ogromna tabelka wyglądająca mniej więcej tak:
Oczywiście oryginalna tabela jest dużo większa.
Po zebraniu wszystkich danych można zauważyć pewne tendencje. Np.
- w niektórych miastach ginie więcej samochodów niż w innych.
- niektóre modele samochodów giną znacznie częściej niż inne.
- samochody częściej kradzione są spod bloku niż z garażu.
- itp.
Dzięki temu znając parametry konkretnego samochodu np. 3 letnia Skoda Octavia Adama, pracownik PZU jest w stanie znaleźć informacje o wszystkich kradzieżach samochodów o takich samych parametrach, garażowanych w takich samych warunkach. Wiedząc ile kradzieży dotyczyło samochodów podobnych do Skody Adama, można łatwo policzyć prawdopodobieństwo tego, że samochód Adama zostanie ukradziony w ciągu najbliższego roku.
Jeśli jest to wartość np. 0,2%, oznacza to, że w ciągu najbliższego roku na każdy 1000 samochodów o parametrach zbliżonych do tych, które ma samochód Adama zostaną ukradzione ok. 2 sztuki.
Oczywiście PZU nie zna przyszłości i nie potrafi wskazać, które 2 samochody zostaną ukradzione, ale tabela z danymi historycznymi pokazuje, że każdego roku zdarzają się mniej więcej 2 kradzieże tego typu aut na każdy 1000 pojazdów poruszających się po drogach.
Wiedząc jakie jest prawdopodobieństwo kradzieży samochodu Adama, PZU ma już prostą drogę do obliczenia składki za ubezpieczenie. Musi być ona taka, aby wpłaty 1000 osób z podobnymi samochodami pokryły koszty wypłat ubezpieczenia dla 2 osób. Do tego trzeba jeszcze doliczyć jakiś bufor bezpieczeństwa i swoją marżę, ale same obliczenia są już bardzo łatwe.
Sposób jest prosty, ale działa od dziesięcioleci i to właśnie dzięki takiemu podejściu do wyceny ubezpieczeń, PZU (i inni ubezpieczyciele) regularnie zarabiają pieniądze.
Dokładnie w taki sam sposób można podejść do wielu innych tematów. Łącznie z inwestowaniem na giełdzie.
- Tak samo jak każdy samochód ma swoje parametry (marka, model, rocznik itp.), tak każda spółka ma swoje parametry (C/Z, ROE, zadłużenie itp.)
- Tak samo jak dla kradzieży samochodów można stworzyć tabelę historii, tak dla spółek można stworzyć analogiczną, która będzie pokazywała, jakie spółka miała parametry i jak przełożyły się one na przyszłe zyski.
- Przy samochodach, jedne parametry mają duże znaczenie dla wyceny ubezpieczenia (np. to czy osiedle jest strzeżone czy nie), a inne tylko wprowadzają szum (np. kolor karoserii samochodu). Tak samo przy spółkach, jedne parametry mają duże znaczenie dla przyszłych zysków (np. C/Z), a inne tylko wprowadzają szum (np. dynamika zmian aktywów).
- Umiejętne połączenie ważnych parametrów pozwala agentom ubezpieczeniowym określać jakie jest prawdopodobieństwo kradzieży samochodu. Umiejętne połączenie ważnych parametrów pozwala inwestorom określać jakie jest prawdopodobieństwo zysku danej spółki.
Cała idea jest banalnie prosta. Aby skutecznie inwestować należy sprawdzać jak w przeszłości zachowywały się spółki o podobnych parametrach do tych, które ma aktualnie spółka, którą zamierzamy kupić. Tylko tyle i aż tyle. Kluczem tu jest obszerna baza z informacjami na temat historycznego powiązania parametrów spółek z ich dalszym zachowaniem.
Aby nie być gołosłownym sprawdziłem czy na pewno można tę samą technikę zastosować do zarabiania w innych branżach. Za swoje pole testowe obrałem pożyczki społecznościowe. Polegają one na tym, że osoby chętne do wzięcia pożyczki, rejestrują się w serwisie i podają swoje dane (wiek, obciążenia kredytowe, rodzaj zatrudnienia itp.). My jako inwestor / pożyczkodawca, możemy przebierać w takich ofertach i decydować komu chcemy udzielić pożyczki. Jeśli wybierzemy dobrze, to naszą nagrodą są dodatkowe odsetki od spłaconej pożyczki. Jeśli jednak trafimy na oszusta, który nie spłaci ani grosza, tracimy całą pożyczoną kwotę.
Tym temat zacząłem się interesować już w kwietniu 2010 roku. Obliczyłem wtedy, że teoretycznie można by w ten sposób zarabiać 34,7% rocznie. Pierwsze kilka miesięcy zeszło na testy różnych podejść, aż w końcu w okolicach lipca 2011 zebrałem wszystkie dane historyczne na temat dotychczas udzielonych pożyczek w ramach serwisu Kokos (kilkanaście tysięcy pożyczek). Informacje te zawierały dane (parametry) pożyczkobiorcy (wiek, obciążenia kredytowe itp.), a także informację, czy pożyczka została spłacona czy nie. Dzięki temu dokładnie tak jak agenci ubezpieczeniowi w PZU, sprawdziłem, które parametry sprzyjają spłacalności pożyczek, które ją zmniejszają, a które są tylko szumem.
Następnie na tej podstawie ustaliłem kryteria, które musi spełniać pożyczkobiorca, aby była bardzo duża szansa, że odda pieniądze. Od tego momentu pożyczałem tylko tym, którzy spełniali moje kryteria. Pisałem o tym nieco więcej w październiku 2011 (a więc niemal rok przed rozpoczęciem prowadzenia fundamentalnego portfela :).
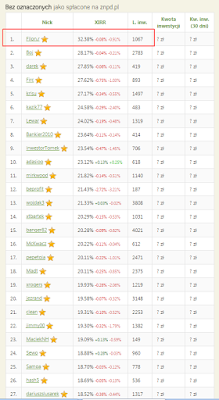
Od czasu opracowania kryteriów oceny pożyczkobiorców korzystałem z tej metody przez ok. 3 kolejne lata. W tym czasie udzieliłem ponad 1000 pożyczek. Mimo iż obecnie od dłuższego czasu pozostaję bierny i przerzuciłem się na inwestowanie na giełdzie, to aktualna tabela z wynikami wciąż plasuje moje konto na pierwszym miejscu w całej Polsce z zyskiem rocznym na poziomie 32%.
Co ciekawe wartość tak jest bardzo bliska obliczonej 5 lat temu teoretycznej wartości możliwej do zarobienia (+34,7% rocznie).
Nie chodzi tu jednak o chwalenie się wynikami, ale o pokazanie, że dokładnie ten sam mechanizm, który pozwala agentom PZU szacować prawdopodobieństwo kradzieży samochodu, pozwala także szacować prawdopodobieństwo, że dana osoba spłaci pożyczkę. I jest to też dokładnie ten sam mechanizm, który pozwala szacować prawdopodobieństwo, że kurs akcji danej spółki wystrzeli w górę.
Co więcej, jeśli pamiętacie ostatni artykuł o decydowaniu czy zezwolić danemu więźniowi na zwolnienie warunkowe, to poprawę wyników uzyskano tam właśnie dzięki zastosowaniu dokładnie tego samego zjawiska.
Warto też pamiętać, że tak jak agent ubezpieczeniowy nie musi wiedzieć, które dwa samochody zostaną ukradzione, aby zarabiać. Tak samo udzielając pożyczek nie musimy dokładnie wiedzieć, które osoby są oszustami, aby zarabiać. I tak samo inwestując na giełdzie, nie musimy wiedzieć dokładnie, które spółki wystrzelą w górę, aby regularnie zarabiać.
Jestem ciekaw co sądzicie o takim podejściu? Znacie jeszcze jakieś branże, w których ludzie wykorzystują duże ilości danych historycznych do zarabiania?
| Jeśli wpis Ci się podoba zapisz się na newsleter, aby nie przegapić nowych artykułów: | Zapisz się |




Brak komentarzy:
Prześlij komentarz